Toward the Ideal Elevator Display

I have raised this blog from the dead to tell of the untapped aesthetic potential of seven-segment displays — the digital displays used in calculators, microwaves, and elevators. Imagine you’re riding an elevator up from the first floor, watching the numbers tick up as you go. You will see something like this:

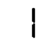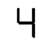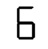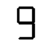
The transition from 2 to 3, effected by a single segment sliding to the right, is immensely satisfying. But this moment of bliss is fleeting. The transition from 3 to 4 is an abomination! There’s another great moment when 5 transforms into 6 via the addition of a single segment, but this too is short-lived: Nearly all the segments disappear in the transition to 7, only to immediately return. All told, it’s a chaotic mess.

Do you find this as distressing as I do? Do you dream of a world where every moment gazing at an elevator display could be as sublime as the transitions from 2 to 3 or 5 to 6? If so, this post is for you. I will dispense with numerical ordering and try to find the most pleasing sequence of characters on a seven-segment display.

If we only have the numerals 0 — 9 to work with, our options are pretty limited. So let’s expand our character set to include other meaningful symbols that can be unambiguously represented on a seven-segment display: the uppercase letters A, C, E, F, H, L, P, and U, the lowercase letters b, d, and h, and the uppercase Greek letters Γ (Gamma) and Π (Pi).¹I chose to exclude lowercase o, c, n, and u because characters that only occupy half of the vertical space of a seven-segment display look wrong to me. Don’t like it? Write your own blog post! Finally, we can sneak in two extra numerals. One is the “reverse P” version of the number 9, which is orthographically distinct from the “upside-down 6” version normally used in seven-segment displays. The other is a 1 that uses the left segments instead of the right segments. Sorted by number of segments, our alphabet now looks like this:

The space of possible sequences here is vast. To make our task more tractable, I will focus on two specific questions, inspired respectively by the 5 —> 6 and 2 —> 3 transitions. First, what’s the best sequence of transitions that connects a 1 to an 8 by adding one segment at each step? Second, what’s the best sequence of transitions that cycles through the 5-segment characters by moving one segment at each step?

The first question is easier to answer. Left-side 1 is a more promising starting point than right-side 1, because more characters open toward the right than toward the left. At the other end of the trajectory, 6 and A are the only viable routes to 8. There are several valid sequences, including two that don’t share any intermediate characters. That means we can build a sequence that loops!

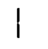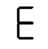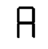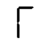
This is a thing of beauty. It could find application in an elevator that moves along the rim of a giant wheel-shaped building — architects take note! We’ve gone above and beyond the goal we set in question 1, and there’s no way to do better.

Question 2 is trickier, and evaluation feels more subjective. The best looping sequence I could find is this one:

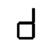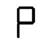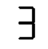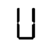
This sequence has an undulatory character that I find very compelling. Unfortunately, there’s no way to fit in an H. Here’s the best sequence I could find that uses all the 5-segment characters:

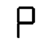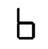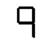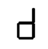
This one doesn’t loop, but d —> P is still among the better transitions that doesn’t satisfy our “move one segment” criterion. Also, it contains the sublime subsequence U —> H —> Π, which is the perfect symbolic encapsulation of an elevator ride.

Here are all three sequences, unfurled for closer inspection:

You can see that the d2EP section of the first 5-segment sequence is reflected on the other side of the Π as 935b, and likewise reflected across the U. It’s like a hall of mirrors with Π and U as the walls! This symmetry is what makes this sequence so pleasing.

The second 5-segment sequence is less symmetric, and unfortunately there’s a fundamental reason for that. In our previous sequence, we got to exploit left/right mirror symmetry, which works really nicely with our alphabet. But to get a sequence that’s symmetric around UHΠ, you’d need to use either vertical reflection symmetry (which leaves E and 3 unchanged) or 180° rotation symmetry (which leaves 2 and 5 unchanged). That means there’s no way to use these characters exactly once in a sequence exhibiting the corresponding symmetry.

Symmetry aside, the second sequence wins the “best subsequence” award. As far as I’m concerned, every three-story building with an elevator should relabel its floors U, H, and Π.

There are surely many longer sequences that combine addition and movement of segments, along with other pleasing transitions, to great effect. Go forth and find them!